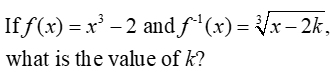Inverse Functions

Basically, to find the "inverse" of a function, the inputs (x) and outputs (y) exchange places.
Think of the coordinates of the graph in a table, and then flip each x with its y-value.

Graphically, the inverse will be a reflection of the original graph over the identity line y = x.
Remember that not all inverses are "functions". Some are simply "relations".

1. Graphing an Inverse Function:
 
Graph the inverse of   y = 2x

 

Start a new Document: Graph

1. Graph f1(x) = 2x

2. To get the calculator to graph the inverse, use the "relation" feature.
Press , #3: Graph Entry/Edit, #2: Relation

     

This step can also be accomplished by hitting
+ G for the relation entry line to appear.


3.  Type x = f1(y) and .
(to get f1, use the key)
This will force the calculator to switch the x and y values.

4. The graph of the inverse of the starting function
will appear.
Note: The graph of line y = x was added to the graph to show the inverse as the reflection of f1 over this line.

 

2.
Check your Answer to a Short Response Question:
 

 

 

First, let's think about what is happening in this problem.
• We start with "x3 with a subtraction of 2".
• If we reverse that process to "undo" these procedures we have "the addition of 2, then a cube root of it all". So we assume the solution will be:
and the value of k = -1.

Now, the calculator can verify the solution to this problem,

We will base our calculator work on the assertion that if you compose a function with its inverse, you get the Identity Function (y = x).

• Graph f (x) and our answer for the inverse f -1(x).

• Graph the Identity Function, y = x.

• Graph the composition of the f (x) and f -1(x).
The composite will be f1(f2(x)).
(to get f1 and f2, use the key)

• Does the composite overlap the Identity Function?

In the diagrams, you can see that the "pink" composite line overlapped the "black" Identity Function line.

This tells us that we have a correct answer for the inverse.
You may to need change your settings.
You need to be in "Real" mode to see the negative x-values for cube roots which will be needed for the inverse function. , #2 Document Settings,
Real or Complex
(arrow until you hit Real). OK

CHECK our ANSWER:

Graph f (x) and our reasoned answer
for f -1(x). Add the graph of y = x.
Now, if we graph the composition of the functions, the new graph should fall on top of y = x.
To graph the composite, use the key.

 

3.
Finding the Answer to a Multiple Choice Question.
 
Choose: 1) 1    2) 2     3) -1     4) -2

 

 

 

Let's take another look at this question from a slightly different perspective. In this solution, we are going to let the calculator try to find the answer to this question.

• Graph the two functions, using the letter k in the inverse function.

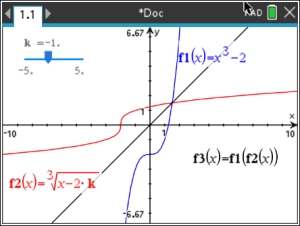
• When the calculator suggests a "slider', say OK.

• As we did in Example 2, we will again use the fact that if you compose a function with its inverse, you get the Identity Function (y = x).
Graph the composition: f1(f2(x)).
Use the key to get those variables, f1 and f2.

• Now use the slider on the values of k to move the composite line.

• Remember that the composite line needs to be the Identity Function, y = x, passing through the origin.

• Since we have four possible answers, focus on those values for k. Move the slider until the composite line goes through the origin. Do you get the appearance of a reflection in this line? YES

The only choice among the four possible answers that puts the composite line through the origin is k = -1.
Answer: Choice 3

While this is a "nice" process, it would be more difficult to determine the exact answer if the possible choices were not given.

 Using the Calculator to Find
the Answer
Graph f (x) and f -1(x).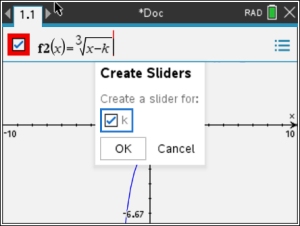
When you enter a variable that is not "x", the calculator asks if you want to add a slider to move values for "k", Hit OK.


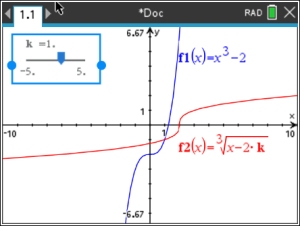
When the slider box appears, move it to the upper left corner, out of the way.
The slider starts with k = 1.


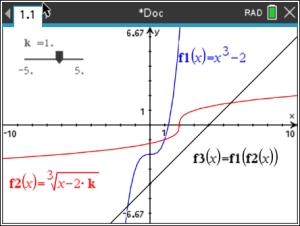
Graph the composite function.
Use the slider to move the composite line to go through the origin and display a reflection in the line.


divider
Table of Contents | MathBits.com | Terms of Use

Table of Contents MathBits.com Terms of Use TI-84+ Web Site